16. Serie-opteller#
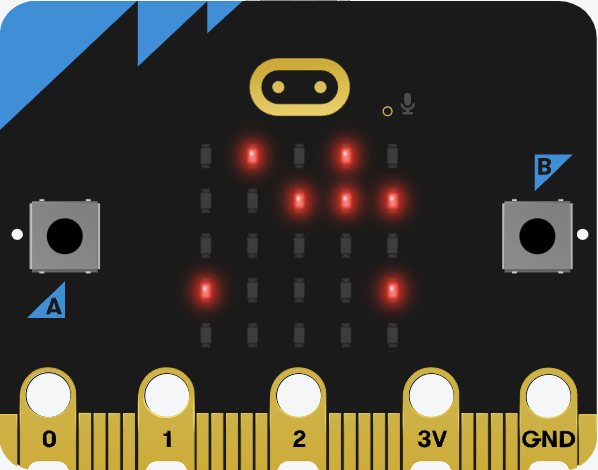
Fig. 16.1 Serie-opteller#
In deze opdracht werk je met een seriële opteller op de microbit, voor het optellen van twee binaire getallen. Serieel wil zeggen dat je de optelling bit-voor-bit uitvoert, van rechts naar links, zoals je ook gewend van het optellen van decimale getallen. De getallen kunnen willekeurig lang zijn. Op de microbit zie je alleen de eerste 4 bits van de getallen en 5 bits van het resultaat: het display is niet groter.
<---| begin rechts
X: 01010
Y: 00111
-----
som: 10001
16.1. Gebruik van het programma#
Installeer het programma op de microbit
Kopieer Het programma hieronder naar de microbit Python-editor, en laad het naar je microbit. (Of voer het uit in de simulator.)
Je gebruikt het programma op de microbit als volgt:
Voor het optellen van twee binaire getallen X en Y voer je steeds het volgende bit van X en het bijbehorende bit van Y in; daarbij werk je van rechts naar links. (Op dezelfde manier als wanneer je twee decimale getallen optelt.) Voorbeeld: voor de getallen hierboven: 0,1, 1,1, 0,1, 1,0
Voor de invoer van een bit gebruik je de knoppen A(0) en B(1). Het bovenstaande voorbeeld wordt dan: A,B, B,B, A,B, B,A.
Zodra je weer twee bits ingevoerd hebt, verschijnt op het display het resultaat van de optelling, en schuift de invoer en uitvoer één positie naar rechts. Uiteindelijk schuift dit “uit het display”, omdat dit display maar een beperkte breedte heeft (5 posities).
Vraag 16.1
Reken zelf uit: 1010 plus 1100 is: (binair). Controleer dit met de microbit. Decimaal is het resultaat: .
feedback???
Vraag 16.2
Met deze opteller kun je willekeurig grote getallen optellen: je moet er dan alleen voor zorgen dat je de bits van het resultaat opschrijft voordat deze uit het microbit-display schuiven.
Reken op deze manier uit: 1010 1010 plus 0100 1100. Dit geeft als resultaat: . (Geef het resulaat in groepjes van 4 bits gescheiden door een spatie.) Decimaal is dit: 170 plus 76 is 246.
feedback?
16.2. Optellen met een eindige automaat#
Deze serie-opteller is gebaseerd op de volgende eindige automaat:

Fig. 16.2 Serie-opteller. ‘a’ staat voor knop A, ‘b’ voor knop B. De notatie ‘b/01’ betekent: bij indrukken van knop B, genereer uitvoer 01.#
Opdracht. Gan na dat er steeds na tweemaal indrukken van een knop (A of B) uitvoer gegenereerd wordt.
Deze automaat geeft een (erg eenvoudig) algoritme voor het optellen van 2 binaire getallen, op basis van de invoer- en uitvoer-symbolen (vormen). Merk op dat er nergens in dit algoritme een “+” voorkomt: het werkt volledig op basis van de vormen. Dit is een voorbeeld van rekenen als “schuiven met vormen, volgens bepaalde regels” - waarbij die vormen verder niet geïnterpreteerd worden.
Deze automaat werkt als volgt:
de toestanden c0 en c1 geven aan dat de “carry” (overdracht) van de vorige optelling 0 of 1 was. (c1 betekent: “1 onthouden” van de vorige optelling.)
s0 staat voor “som tot nu toe: 0”, na de invoer van 1 symbool (het bit van X), s1: “som is 1”, s2: “som is 2”
bij de invoer van elk 2e symbool (het bit van Y) vindt de output van de som plaats, en is de nieuwe toestand c0 of c1, afhankelijk van het cijfer dat onthouden moet worden.
de uitvoer “01” betekent: 0 onthouden (overdracht), vul in: 1.
16.3. Van automaat naar programma#
De bovenstaande automaat kun je op een systematische manier omzetten naar een programma. Hiervoor zet je de automaat eerst om in tabelvorm.
Deze automaat in tabelvorm:
state |
input |
output |
next |
|---|---|---|---|
c0 |
a |
s0 |
|
c0 |
b |
s1 |
|
s0 |
a |
0 |
c0 |
s0 |
b |
1 |
c0 |
s1 |
a |
1 |
c0 |
s1 |
b |
0 |
c1 |
c1 |
a |
s1 |
|
c1 |
b |
s2 |
|
s2 |
a |
0 |
c1 |
s2 |
b |
1 |
c1 |
Sorteren op input, in plaats van op state, geeft:
state |
input |
output |
next |
|---|---|---|---|
c0 |
a |
s0 |
|
s0 |
a |
0 |
c0 |
s1 |
a |
1 |
c0 |
c1 |
a |
s1 |
|
s2 |
a |
0 |
c1 |
c0 |
b |
s1 |
|
s0 |
b |
1 |
c0 |
s1 |
b |
0 |
c1 |
c1 |
b |
s2 |
|
s2 |
b |
1 |
c1 |
In programmavorm wordt dit:
def handle_a():
if state == c0:
state = s0
elif state == s0:
state = c0
output_sum(0, 0)
elif state == s1:
state = c0
output_sum(0, 1)
elif state == c1:
state = s1
elif state == s2:
state = c1
output_sum(1, 0)
def handle_b():
if state == c0:
state = s1
elif state == s0:
state = c0
output_sum(0, 1)
elif state == s1:
state = c1
output_sum(1, 0)
elif state == c1:
state = s2
elif state == s2:
state = c1
output_sum(1, 1)
state = c0
while True:
if button_a.was_pressed():
handle_a()
if button_b.was_pressed():
handle_b()
Dit is de kern van het programma. De rest is alleen nodig voor de uitvoer naar het microbit-display.
Opdracht 16.1 (uitbreiding)
Onder het resultaat is nog een lege regel in het display. Pas het programma zo aan dat je een 10-bits resultaat kunt weergeven.
16.4. Het programma#
from microbit import *
# microbit output for serial adder
next_is_x = True
inputs_x = [0, 0, 0, 0, 0]
inputs_y = [0, 0, 0, 0, 0]
outputs = [0, 0, 0, 0, 0]
def input_bit(bit):
global next_is_x, inputs_x, inputs_y
if next_is_x:
inputs_x[0] = bit
else:
inputs_y[0] = bit
next_is_x = not next_is_x
def output_sum(b1, b0):
global inputs_x, inputs_y, outputs
print(b1, ",", b0)
outputs[0] = b0
inputs_x.insert(0, 0)
inputs_x.pop(5)
inputs_y.insert(0, 0)
inputs_y.pop(5)
outputs.insert(0, b1)
outputs.pop(5)
display_state()
def display_state():
display.clear()
for i in range(5):
display.set_pixel(i, 0, inputs_x[i]*9)
display.set_pixel(i, 1, inputs_y[i]*9)
display.set_pixel(i, 3, outputs[i]*9)
# the actual serial adder
c0 = 0 # states of the automaton
c1 = 1
s0 = 2
s1 = 3
s2 = 4
state = c0
def handle_a():
global state
if state == c0:
state = s0
elif state == s0:
state = c0
output_sum(0, 0)
elif state == s1:
state = c0
output_sum(0, 1)
elif state == c1:
state = s1
elif state == s2:
state = c1
output_sum(1, 0)
def handle_b():
global state
if state == c0:
state = s1
elif state == s0:
state = c0
output_sum(0, 1)
elif state == s1:
state = c1
output_sum(1, 0)
elif state == c1:
state = s2
elif state == s2:
state = c1
output_sum(1, 1)
def reset():
global state, next_is_x, inputs_x, inputs_y, outputs
state = c0
next_is_x = True
inputs_x = [0, 0, 0, 0, 0]
inputs_y = [0, 0, 0, 0, 0]
outputs = [0, 0, 0, 0, 0]
display_state()
reset()
while True:
if button_a.was_pressed():
input_bit(0)
handle_a()
if button_b.was_pressed():
input_bit(1)
handle_b()
if accelerometer.was_gesture('shake'):
reset()
sleep(20)
