input-output systemen

(Misschien combineren met signalen en events.)

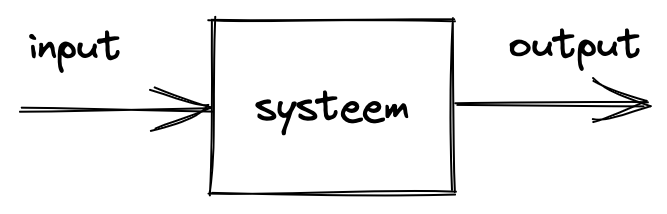
Fig. 7 Input-output systeem

Een microbit, met sensoren, actuatoren en microcontroller, is een voorbeeld van een input-output-systeem. De microcontroller genereert voor elke sensor-input via de actuatoren de bijbehorende output.

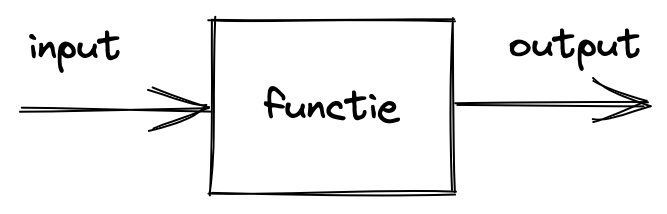
Fig. 8 Functioneel input-output systeem

Het verband tussen de input en de output kan functioneel zijn (als bij functioneel programmeren, of in de wiskunde): de output op een bepaald tijdstip hangt dan alleen af van de input op dat tijdstip. (Voorbeeld: een klassieke deurbel: deze maakt alleen geluid op het moment dat je de knop indrukt.)

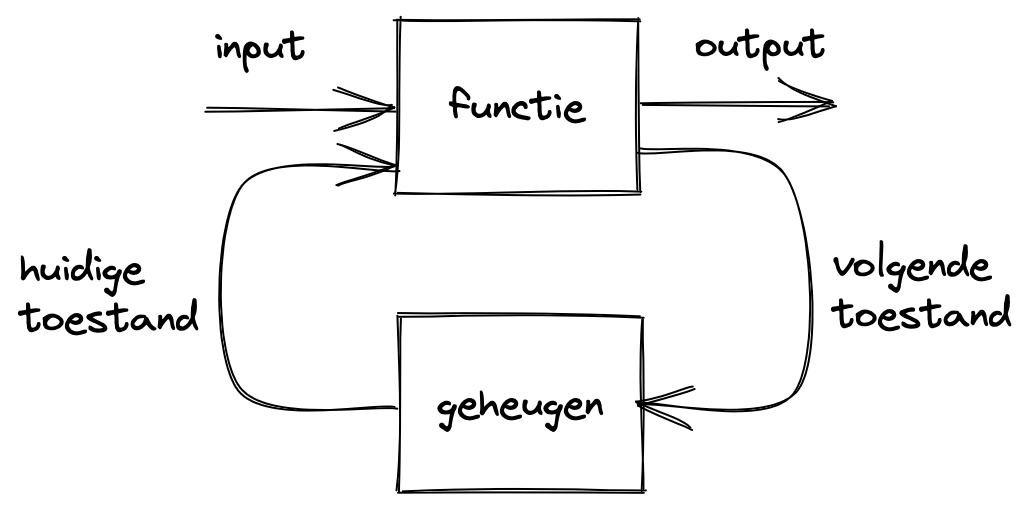
Fig. 9 Input-output systeem met geheugen (toestand)

Wat vaker voorkomt is dat de output op een bepaald tijdstip functioneel afhangt van de input en van de toestand op dat moment. Ook de volgende toestand hangt dan af van de huidige input op dat moment en van de huidige toestand. Dit is een systeem met geheugen: de toestand vormt een samenvatting van de voorgeschiedenis.

In formules kun je dit beschrijven als:

\[ o_{t_{n}} = F(o_{t_{n}}) \]

\[ o_{t_{n}} = F(i_{t_{n}}, s_{t_{n}}) \]

\[ s_{t_{n+1}} = G(i_{t_{n}}, s_{t_{n}}) \]

Hierin is \(o_{t_{n}}\) de output op tijdstip \({t_{n}}\), \(i_{t_{n}}\) de input op tijdstip \({t_{n}}\), en \(s_{t_{n}}\) de toestand op tijdstip \({t_{n}}\). \(F\) en \(G\) zijn hierin functies (zoals in de wiskunde, of in functioneel programmeren).

Je kunt de bovenstaande figuren zowel gebruiken voor signalen als voor events. In het geval van events beschrijft de tweede figuur een eindige automaat. In het geval van signalen beschijft deze tweede figuur een signaal-regeling, zoals een PID-controller (