Cellulaire automaten#

Een 1-dimensionale cellulaire automaat bestaat uit een reeks aaneengesloten cellen. Een cel is “levend” (zwart, 1) of “dood” (wit, 0). De toestand van een automaat op een bepaald moment geeft aan welke cellen levend zijn, en welke dood. Dit kun je weergeven als een (horizontale) rij zwart/witte cellen (hokjes).

../_images/automaton-state.png

Fig. 1 Toestand van een cellulaire automaat#

Gegeven een toestand van een automaat, kun je voor elke cel de volgende toestand bepalen uit de toestand van die cel en die van zijn directe buren. Je kunt de opeenvolging van toestanden weergeven door deze onder elkaar te tekenen, in een plat vlak.

Voorspel de volgende toestanden. Bekijk de volgende reeks toestanden, waarbij de rijen 4 en 5 nog niet ingevuld zijn:

../_images/automaton-sequence.png

Fig. 2 Opeenvolging van toestanden#

Kun je voorspellen welke waarden je krijgt in rijen 4 en 5?

Vraag 1

Geef de waarden voor rij 4 en rij 5 als een reeks van 0-en en 1-en, 0 voor wit en 1 voor zwart. Deze rij moet 9 tekens lang zijn.

Rij 4:

Rij 5:

Tip: bepaal voor elke combinatie van een cel met zijn directe buren, wat de volgende toestand is voor die cel: welke waarden moeten er staan op de plek van de vraagtekens? Dit zijn de regels van de cellulaire automaat.

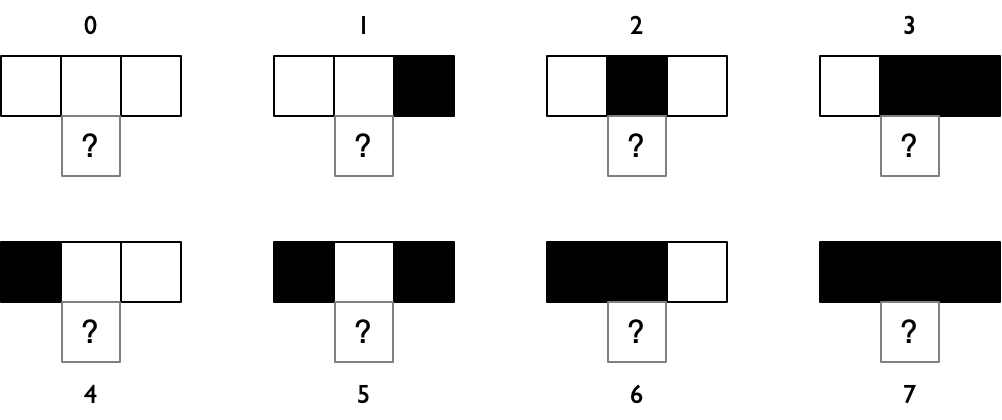
../_images/automaton-rules-empty.png

Fig. 3 Welke regels voor de volgende toestand van een cel?#

Vraag 2

Het resultaat kun je beschrijven als een reeks 0-en en 1-en, 0 voor wit en 1 voor zwart, in de volgorde van linksboven (0) naar rechtsonder (7). Geef hier het resultaat:

Bepaal met de onderstaande regels de toestand in rij 4, en vervolgens in rij 5.

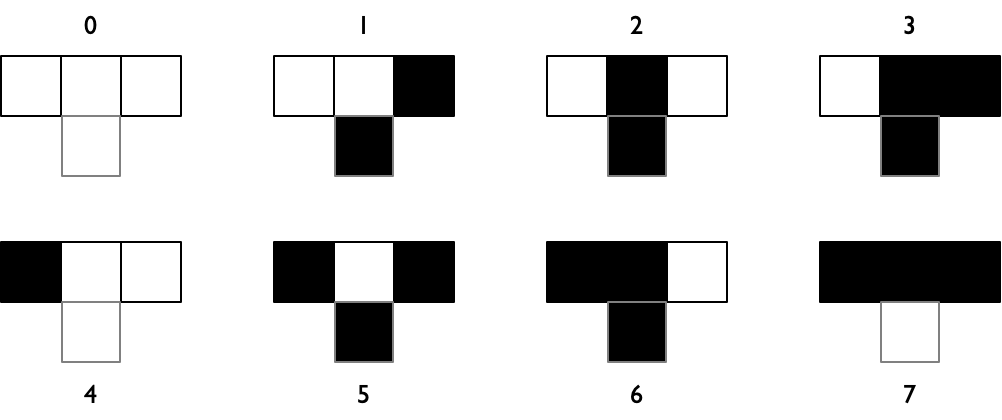
../_images/automaton-rules.png

Fig. 4 Regels voor de volgende toestand van een cel#

Het resultaat:

../_images/automaton-sequence-complete.png

Fig. 5 Stappen 4 en 5 ingevuld.#

Als je de regels van de cellulaire automaat kent, kun je uit elke toestand de volgende toestand uitrekenen. Er zijn 8 regels (maximaal): één voor elke combinatie van de toestand van een cel en die van zijn buren. Deze 8 regels kun je uitdrukken als een reeks van 8 bits, en die reeks kun je weer zien als een getal.

De cellulaire automaat hierboven heet “regel 110”. Deze automaat heeft een bijzondere eigenschap: deze is “Turing complete”, dat wil zeggen: je kunt er dezelfde berekeningen mee uitvoeren als met een willekeurige andere computer. We hebben eerder gezegd: rekenen is schuiven met vormen, volgens bepaalde regels. Deze regels kunnen dus echt heel eenvoudig zijn!

De vertaling van een rekenprobleem naar deze cellulaire automaat is wel ingewikkeld: het is niet een praktische oplossing. Maar dat doet aan de fundamentele rekenkracht van deze automaat niets af.

Meer weten?

Programma#

Hieronder geven we een programma voor het uitrekenen van de opeenvolgende toestanden van een cellulaire automaat, in Python.

import random
from typing import List

rule = [0, 0, 0, 0, 0, 0, 0, 0]  # rule represented as 8 bits

size = 10     # number of cells in a state
state = []    # a list of cells
history = []  # a list of states

# create a new cellular automaton
# nr_cells: number of cells
# ones:     positions of living cells
def create_state(nr_cells: int, ones: List[ int ]) -> None:
    global size, state, history
    size = nr_cells
    state = []
    for i in range(size):
        if i in ones:
            state.append(1)
        else:
            state.append(0)
    history = [state]

# set rule-list from rule-number
def set_rule(rulenr: int) -> None:
    global rule
    for r in range(8):
        rule[r] = rulenr % 2
        rulenr = rulenr // 2

# cell-value in current state,
# with border-cells with value 0
def cell(i: int) -> int:
    if i < 0 or i >= len(state):
        return 0
    else:
        return state[i]

# compute next state
# and add to history
def step_state() -> None:
    global state, history
    next_state = []
    for i in range(size):
        cell_state = cell(i-1) * 4 + cell(i) * 2 + cell(i+1)
        next_state.append(rule[cell_state]) 
    state = next_state
    history.append(state)

def display_history() -> None:
    for row in history:
        line = ""
        for x in row:
            line = line + str(x)     
        print(line)

Tip

Je kunt deze pagina “live” maken, via het menu raket->Live code bovenin. De code-cellen krijgen dan knoppen waarmee je deze uit kunt voeren. Je kunt de code in de cellen ook aanpassen, voor eigen experimenten. Let op: het opstarten van een “live book” kan even duren; als je dan een cel probeert uit te voeren, krijg je de melding “waiting for kernel”.

Met “Live code” kun je de code op deze pagina aanpassen en opnieuw uitvoeren. Voer eerst de code-cel hierboven uit; daarna kun je de begintoestand of de regel hieronder aanpassen en de cellulaire automaat een aantal stappen laten uitvoeren.

create_state(40, [20,22,24])
set_rule(110)
for i in range(20):
    step_state()
display_history()

0000000000000000000010101000000000000000
0000000000000000000111111000000000000000
0000000000000000001100001000000000000000
0000000000000000011100011000000000000000
0000000000000000110100111000000000000000
0000000000000001111101101000000000000000
0000000000000011000111111000000000000000
0000000000000111001100001000000000000000
0000000000001101011100011000000000000000
0000000000011111110100111000000000000000
0000000000110000011101101000000000000000
0000000001110000110111111000000000000000
0000000011010001111100001000000000000000
0000000111110011000100011000000000000000
0000001100010111001100111000000000000000
0000011100111101011101101000000000000000
0000110101100111110111111000000000000000
0001111111101100011100001000000000000000
0011000000111100110100011000000000000000
0111000001100101111100111000000000000000
1101000011101111000101101000000000000000